Event-learning with a background controller can be formulated as an $\varepsilon$-MDP

Lemma D.1 (Corollary 4.3)   Assume that the environment is such that $\sum_y \vert P(x,u_1,y) - P(x,u_2,y)\vert \le K \Vert u_1 - u_2\Vert$ for all $x,y,u_1,u_2$. Let $\varepsilon$ be a prescribed number. For sufficiently large $\Lambda$ and sufficiently small time steps, the SDS controller described in Equation 10 and the environment form an $\varepsilon$-MDP.

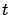
Proof. From [Szepesvári et al.(1997)] it is known that for sufficiently fine time steps, the eventual tracking error is bounded by $\textit{const}/\Lambda$, i.e., for sufficiently large $t$,

$$\Vert U_t(x,y^d)-U(x,y^d)\Vert \le \frac{\textit{const}}{\Lambda}.$$

For sufficiently large $\Lambda$, $\textit{const}/\Lambda \le \varepsilon$. Therefore for arbitrary value function $S$ we may write

$$\Vert {\textstyle\bigotimes}_t {\textstyle\bigoplus}_t S - {\text... ...plus}S \Vert \le \Vert {\textstyle\bigoplus}_t S - {\textstyle\bigoplus}S \Vert$$

$$\le \left\Vert \sum_y \sum_u (\pi_t^A(x,y^d,u) - \pi^A(x,y^d,u)) P(x, u, y) S(x,y^d,y)\right\Vert$$

$$= \left\Vert \sum_y \left( P(x, U_t(x,y^d), y) - P(x, U(x,y^d), y) \right) S(x,y^d,y)\right\Vert$$

$$\le \sum_y \vert P(x, U_t(x,y^d), y) - P(x, U(x,y^d), y)\vert \cdot \left\Vert S \right\Vert$$

$$\le K \Vert U_t(x,y^d)-U(x,y^d)\Vert \cdot \Vert S\Vert \le \varepsilon \cdot \Vert S\Vert.$$

This means that the system is indeed an $\varepsilon$-MDP. $\qedsymbol$

Naturally, if $\pi^A = \pi^A_*$ then the approximated value function will be $E^*$.