


Next: Comparison with TBL:
Up: First Experiment
Previous: The effect of refinement:
As Table 4 shows, a majority of rules have a small coverage relatively to the size of the training data.
The rules with a coverage lesser or equal to 5 represent 63% of the rules.
But rules covering only a few cases of the training data can perform relatively badly since they have inadequate statistical support.
This problem has been referred to in the literature as the small disjuncts problem by [Holte et al.(1989)Holte, Acker, and Porter].
Several results, [, see][]Holte_1989,holder-unifying,provost97survey,ali95reducing show that accuracy decreases with the addition of small disjuncts.
Table 4:
Evolution of F1-score using low frequency rules (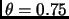 ,lg=2).
,lg=2).
| Coverage |
nb rules |
Precision |
Recall |
F1 |
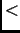 3 3 |
174(13%) |
+0.47% |
+0.28% |
+0.37 |
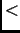 6 6 |
880(63%) |
+1.17% |
+0.75% |
+0.96 |
|
But Table 4 indicates that, in our experiment, the rules with low frequency (lesser or equal to 5) provide a substantial improvement of the F1-score.
Even rules with a frequency of 2, which can be considered as the least reliable, improve the F1-score.
Whatever the value of the other parameters, low frequency rules have to be learned for this data.
In fact, our result is not in contradiction with the previous ones.
[Holte et al.(1989)Holte, Acker, and Porter] conclude that if the small disjuncts are specific enough, their error rate decreases considerably.
This is in fact a specificity of our rules with low frequency, which are very specific, almost describing a lexicalized context.
Note that the coverage of a rule has to be nevertheless greater than 1.



Next: Comparison with TBL:
Up: First Experiment
Previous: The effect of refinement:
Hammerton J.
2002-03-13