Proof.
Define the auxiliary operator sequence
 |
(6) |
where
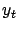
is sampled from distribution

, and

. Note that the only difference between
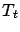
and

is that the successor states (
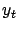
and

) are sampled from different distributions (

and

). By Lemma
B.1, we can assume that

, and at the same time
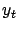
is
sampled from

and

from

(
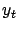
and

are not independent from each
other).
Note also that the definition in Equation 6
differs from that of Equation 5, because
 is not necessarily the successor state of
is not necessarily the successor state of  .
Fortunately, conditions of the Robbins-Monro theorem
[Szepesvári(1998)] do not require this fact, so it remains
true that
.
Fortunately, conditions of the Robbins-Monro theorem
[Szepesvári(1998)] do not require this fact, so it remains
true that 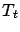 approximates
approximates  at
at  uniformly w.p.1.
uniformly w.p.1.
Let
 be an arbitrary value function, and let
be an arbitrary value function, and let
and
Recall that

-approximation means that

w.p.1.
Since

and

w.p.1, it suffices to show that

w.p.1.
Clearly, for any  ,
,
where we used the shorthand

for

.
Since this holds for every

,
it also does for their maximum,

. As
mentioned before,

. If

,

.
Otherwise the only applicable upper bound is

. Therefore the
following random sequence bounds

from
above:

,
 |
(7) |
where
It is easy to see that Equation
7 is a
Robbins-Monro-like iterated averaging
[
Robbins and Monro(1951),
Jaakkola et al.(1994)]. Therefore

converges
to

w.p.1.
Consequently,
 , which completes the proof.
, which completes the proof.

Theorem 3.5
Let

be the optimal value function of the base MDP of the
generalized

-MDP, and let

. If Assumption A holds, then

w.p.1, i.e., the
sequence


-approximates the optimal value function
with

.
Proof.
By Lemma
3.4, the
operator sequence

-approximates

(defined in
Equation
2) at

with

. The
proof can be finished analogously to the proof of
Corollary
A.3: with the substitution

, and defining

and

as in Equations
11
and
12, the conditions of Theorem
3.3
hold, thus proving our statement.

![]() in the following fashion:
in the following fashion:
![]() -MDP:
-MDP:
![]() is not necessarily the successor state of
is not necessarily the successor state of ![]() .
Fortunately, conditions of the Robbins-Monro theorem
[Szepesvári(1998)] do not require this fact, so it remains
true that
.
Fortunately, conditions of the Robbins-Monro theorem
[Szepesvári(1998)] do not require this fact, so it remains
true that ![]() approximates
approximates ![]() at
at ![]() uniformly w.p.1.
uniformly w.p.1.
![]() be an arbitrary value function, and let
be an arbitrary value function, and let
![]() ,
,





![]() , which completes the proof.
, which completes the proof.
![]()